ISSN: 1204-5357
ISSN: 1204-5357
| LADISLAV BERANEK, PhD MBA, Associate Professor, University of South Bohemia, Faculty of Economics, Ceske Budejovice, Czech republic Postal Address: Studentska 13, 37005 Ceske Budejovice, Czech Republic Email: beranek@ef.jcu.cz |
| Prof. Ladislav Beranek is a member of Department of Applied Mathematics and Informatics at the Faculty of Economics, University of South Bohemia, Czech Republic. His research interests are e-commerce, web technologies, data mining and social network analysis. |
| JIRI KNIZEK, PhD Research Associate, Charles University in Prague, Faculty of Medicine in Hradec Kralove, Department of Medical Biophysics, Hradec Kralove, Czech Republic Postal Address: Simkova 870/13, 50038, Hradec Kralove, Czech Republic Email: knizekj@lfhk.cuni.cz |
| Dr. Jiri Knizek is a member of Department of Medical Biophysics, Faculty of Medicine in Hradec Kralove, Charles University in Prague. His main research interests are statistic methods and their application especially in medicine and biology. |
Visit for more related articles at Journal of Internet Banking and Commerce
Currently, Internet auction portals are an integral part of business activities on the Internet. Anyone can easily participate in online auctions, either as a seller or a buyer (bidder), and the total turnover on Internet auction portals represents billions of dollars. However, the amount of fraud in these Internet auctions is related to their popularity. To prevent discovery, fraudsters exhibit normal trading behaviors and disguise themselves as honest members. It is therefore not easy to detect fraud in online auctions. There are some papers and approaches dealing with this problem with varying results. Most of them concentrate on the selection of the attributes available within online auction portals and on computational methods for their processing. This study proposes extended the fraud detection approach by using certain contextual information whose origin is outside online auctions portals. The suggested model integrates information from auctions and relevant contextual information with the aim to evaluate the behavior of certain sellers in an online auction and determine whether it is legal or not. Experimental results show that this approach based on the use of contextual information from other Internet sources provides good results and enhances significantly the accuracy of detection of certain types of fraud in online auctions.
Keywords |
| online auctions; Internet fraud; information integration; reasoning under uncertainty |
INTRODUCTION |
| Currently, many users participate in online auctions operated by various Internet online auction portals. Besides eBay (eBay, 2013), the Aukro auction portal (Aukro, 2013), a Czech auction company with a turnover of USD 250 million and 2.5 million users as of January 2012, is an example of such an Internet auction system. Online auctions allow their users to buy or sell products and services. A large number of users use Internet auctions as their main source of income. For example the Aukro states (Aukro, 2013) that from 2.5 million users, 9,300 users are professional traders. On the other hand, the amount of a fraud in online auctions is also increasing (Gavish and Tucci, 2006). |
| The most common types of fraud are incorrect (purposely) description of goods, undelivered goods, irredeemable payments, sale of stolen goods, and others (Gregg and Scott 2008). Fraudsters are attracted by low admission costs and high profit potential. A typical procedure for the detection of fraudulent behavior on an online auction consists of the two basic steps: (1) a set of attributes is proposed and their values are extracted from a transaction history to distinguish between normal traders and scammers, and (2) a detection model based on these attributes is built using various machine learning techniques. |
| This study aims to suggest an improvement of detection methods on the basis of utilization of additional sources of information (contextual information). For this purpose, various sources of information on the Internet, which could serve as sources of contextual information and hence could be used to improve the detection of fraud, have been explored. More than 195 different Internet forums and discussions and similar Internet sources were surveyed. Specific pieces of information relating to some Internet auctions were extracted from these information sources and examined in detail. Together with these information sources, we investigated 424 online auctions on the Aukro auction portal (Aukro, 2013). Our proposed fraud detection model was tested with the help of this information. The results of our experiments show that the proposed approach improves the accuracy of fraud detection in online auctions. |
| The remainder of this paper is organized as follows: Section 2 summarizes some concepts and techniques related to the detection of fraud in online auctions including works using the belief function approach. Section 3 presents the basic principles of the belief theory, including a description of a situation when there might be some doubts about the reliability of information sources. Section 4 presents our approach. It outlines the key definitions of belief functions which represent the degree of potential fraudulent behavior. This degree is calculated on the basis of information about the respective online auction and on the basis of contextual information found using other Internet information sources. Contextual discounting is used here to express the influence of contextual information on the degree of potential fraudulent behavior. Section 5 presents the results of the experiments, followed by the conclusion and suggestions for future work in Section 6. |
BACKGROUND AND RELATED WORK |
| Successful Internet auction portals must perform many different activities. In addition to the creation, implementation and operation of their trading system (including users login, displaying data about items being sold, including initial price and duration of auction, displaying of bids of buyers and other data) they must also solve problems with trust and trustfulness. This follows from the fact that transactions in the online auction predominantly take place in a situation when the users do not know each other. However, if users want to do business here they must decide whether they will trust each other. Online auction portals, such as eBay (eBay, 2013), Aukro (Aukro, 2013) and others are successful primarily because they are able to create a trusted environment for users of online auctions (Hoffman et al., 1999; Bryant and Colledge, 2002; Hsu and Wang, 2008). Most of the mechanisms (reputation systems), which create a trusted environment, use a variety of attributes associated with users and their roles. |
Fraudulent Behavior |
| Although reputation systems and certain methods of user identification are functional, a lot of fraud takes place in online auctions. The sellers and bidders are not in physical contact, and bidders are not able even physically see the auctioned item. This situation provides many opportunities for cheating (Chae et al, 2010; Chua and Warenham, 2008; Sukurai and Yokoo, 2003). |
| From the perspective of a seller, online auctions bring about certain risks (Trevathan and Read, 2008, 2009; Gregg and J. Scott, 2008; Dong et al, 2009), particularly: |
| − Bidder does not pay for the goods supplied. |
| − Bidder wrongly claims that the goods have not been delivered. |
| From the perspective of the bidder (Trevathan, 2005): |
| − The seller refuses to send the goods (Gregg and Scott, 2008). |
| − The description of the auctioned object is false. |
| − Seller sends different goods or goods of lower quality (Da Silva Almendra and Schwabe, 2009). |
| − Goods intended for auction are fake or stolen. |
| − Seller can influence the course of the auction (seller can collude with other bidders or can bid on his own items to drive up the price of the item being auctioned) (Trevathan and Read, 2007). We denote this as shill behavior. |
| Fraudulent behavior is relatively widespread in online auctions. The main reason is that engaging in fraudulent behavior is relatively easy because: |
| − Online auction participants are largely anonymous - they frequently act under pseudonyms. Internet auction systems use different methods for verifying the identity of users. These methods, however, may not be sufficiently reliable (Beranek, 2010a). |
| − Online auction houses do not always exhibit full commitment to actively engage in combating fraud. |
| − Law enforcement is often difficult with regard differences of legal systems in different countries. |
Related Work |
| Fraudulent behavior which occurs in online auctions is not easy to detect mainly due to the use of various techniques by fraudsters to camouflage their behavior and due to the pseudonymity of users participating in the auction. The most widely used detection approaches are based on various statistical methods, data mining techniques, methods of analysis of online users behavior or social networks analysis, see for example (Hu and Panda, 2005; Gregg and Scott, 2006, 2008; Chang and Chang, 2012; Ku et al., 2007; Pandit et al., 2007; Zhang et al. 2008; Ku et al.,2007; Zhang et al., 2008) and others. Works that deal with the detection of fraudulent behavior in online auctions focus mostly on certain types of fraudulent behavior, for example shill behavior (Dong et al., 2010; (Trevathan et al., 2009). A general approach would be very complicated due to the complexity of the issue. |
| The selection of an appropriate set of attributes is crucial for constructing a detection model. The simplest way to devise an attribute set for fraud detection is to enumerate all the features of tricks that have already occurred. Attributes of fraudulent behaviors are taken directly from statistics related to past transactions. These attributes include the count of positive ratings and negative ratings, the median, the standard deviation, the average of all labeled prices during a specific time period (Chau and Faloutsos, 2005), the starting labeled price of a bid and some Boolean variables (Wang and Chiu, 2005). Trevathan and Read (2007) deal with fraudulent behavior in online auctions. They propose an algorithm to detect shill behavior based on comparisons of patterns of behavior in online auctions. Trevathan and Read present in another paper (Trevathan and Read 2009) a method for detecting colluding shill users. Chau et al. (2006) use methods based on a data mining approach to detect shill behavior. They apply this approach on the user level and on the level of interaction among users. They link these two levels to detect suspicious behavior patterns using Markov random field methods. Xu and Cheng (2007) introduce a dynamic auction model for shill detection in real online auctions and use formally specified shilling behavior by the help of linear temporal logic to verify the shill behavior. The other authors (Goel et al, 2010, Ford et al, 2010,) propose using Bayesian networks or decision trees to detect fraudulent behavior in online Internet auctions. |
| The use of belief functions to detect shill behavior is presented in the work of Dong et al. (2009, 2010, 2012). The authors indicate a conceptual design framework for calculating the belief functions. They demonstrate the correctness of their approach in an eBay auctions case study. The paper (Beranek et al., 2010b, 2012) describes some features of shill behavior which are then expressed by belief functions and combined with the aim to classify users into categories of shill, suspect and trustworthy. Pandit et al. (2007) designed and implemented an online auction fraud detection system named NetProbe. The NetProbe system models auction data as a network graph in which sellers and bidders are represented by nodes, and transactions between sellers and bidders are represented by edges. The Markov random field and the belief propagation algorithms are utilized to unearth suspicious trading patterns created by fraudsters and thus to detect possible fraudsters. An online auction fraud detection systems was also presented in the works (Chau and Faloutsos, 2005, Chau et al., 2006a,b, Pandit et al. 2007, Zhang et al., 2008, Chang and Chang, 2011). Chang et al. (2012) propose the data mining methods for early detection of fraudulent behavior. Forty-four attributes are defined and analyzed in this paper with the aim to build a model for early detection of fraud. Kwan et al. (2010) focus on the detection of selling fake products. They define attributes of this fraudulent behavior and use the Bayes approach in their evaluation. |
| Generally, the detection accuracy is closely related to the suitability of the attributes and the choice of modeling method. It is obvious that previous work in this area has provided good level of progress but some problems still remain. The use of a greater number of measured attributes may not bring substantial improvement. The accuracy of detection can even deteriorate when irrelevant attributes are incorporated into the model. A major improvement in fraud detection based on data from auction portals cannot be expected at the present. We therefore suggest an improvement of fraud detection on the basis of the utilization of additional sources of information available on the Internet. |
THE PROPOSAL OF OUR MODEL |
| This paper aims to detect specific Internet auction fraud related to the selling of stolen goods (i.e., goods being stolen and subsequently sold in an online auction). The detection model is based on chosen attributes of this fraud and it also uses contextual information, i.e., information found on various public Internet forums and discussions to improve the prediction accuracy of the detection model. The model is based on the belief function theory. The advantage of the use of this theory is the possibility to represent partial knowledge and the possibility to combine pieces of evidence concerning possible fraudulent behavior with pieces of contextual information from the Internet sources. |
Basic Principles of the Belief Function Theory |
| Our model is a particular application of the belief function theory. The belief function theory (Shafer, 1976) is designed to deal with the uncertainty and incompleteness of available information. It is a powerful tool for combining evidence and changing prior knowledge in the presence of new evidence. The belief function theory can be considered as a generalization of the Bayesian theory of subjective probability. In the following paragraphs, we give a brief introduction of the basic notions of the belief function theory (frequently called Dempster-Shafer theory or theory of evidence). Considering a finite set referred to as the frame of discernment Ω a basic belief assignment (BBA) is a function m: 2Ω [0,1] so that |
| where m(∅) = 0, see (Shafer, 1976). The subsets of 2Ω which are associated with nonzero values of m are known as focal elements and the union of the focal elements is called the core. The value of m(A) expresses the proportion of all relevant and available evidence that supports the claim that a particular element of belongs to the set A but not to a particular subset of A. This value pertains only to the set A and makes no additional claims about any subsets of A. We denote this value also as a degree of belief (or basic belief mass - BBM). |
| Shafer further defined the concepts of belief and plausibility (Shafer, 1976) as two measures over the subsets of as follows: |
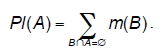 (3) (3) |
| A BBA can also be viewed as determining a set of probability distributions P over so that Bel(A) ≤ P(A) ≤ Pl(A). It can be easily seen that these two measures are related to each other as Pl(A) = 1 - Bel(A). Moreover both of them are equivalent to m. Thus one needs to know only one of the three functions m, Bel, or Pl to derive the other two. Hence we can speak about belief function using corresponding BBAs in fact. |
| Dempster's rule of combination can be used for pooling evidence represented by two belief functions Bel1 and Bel2 over the same frame of discernment coming from independent sources of information. The Dempster's rule of combination for combining two belief functions Bel1 and Bel2 defined by (equivalent to) BBAs m1 and m2 is defined as follows (the symbol ⊕ is used to denote this operation): |
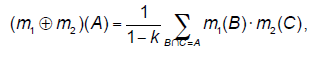 (4) (4) |
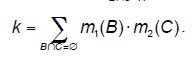 (5) (5) |
| Here k is frequently considered to be a conflict measure between two belief functions m1 and m2 or a measure of conflict between m1 and m2 (Shafer, 1976). Demspter's rule is not defined when k = 1, i.e. when cores of m1 and m2 are disjointed. This rule is commutative and associative; as the rule serves for the cumulation of beliefs, it is not idempotent. |
Belief Function Correction |
| When receiving a piece of information represented by a belief function, some metaknowledge regarding the quality or reliability of the source that provides some information can be available. In the following paragraphs, we describe briefly some possibilities how to adjust the information according to this metaknowledge. |
| Discounting. To handle the lower reliability of information sources, a discounting scheme has been introduced by Shafer (1976). It is expressed by equations: |
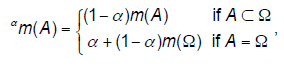 (6) (6) |
| where α∈[0,1] is a discounting factor and αm(A)denotes the discounted mass of m(A). The larger α is, the more mass m(A) is withdrawn from A ⊂ Ω and assigned to the frame of discernment Ω. |
| Thus, the principle of discounting is transferring parts of basic belief masses BBMs of all focal elements which are proper subsets of the frame of discernment to the entire frame. |
| This process is the result of additional information which indicates that the source is not entirely reliable. The transfer of BBMs from a source to the framework reflects an increase of the degree of uncertainty of the data that the source produces. |
| De-discounting (reinforcement). In some cases we need to perform an opposite operation, e.g., transfer parts of basic belief mass (BBM) from the entire frame to all focal elements. This can be the result of a situation when we, for example, obtain information that the source of the information is more reliable than we had anticipated at the beginning. We can then re-compute m by reversing the discounting operation (Smets, 1993; Mercier et al, 2012). We denote this operation as reinforcement (or dediscounting): |
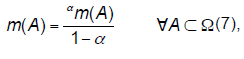 (7) (7) |
 (8) (8) |
| where α α ∈[0, m(Ω)]. We denote here α as a reinforcement coefficient. The result of maximal de-discounting is the totally reinforced belief function. It is noted trm and defined as follows: |
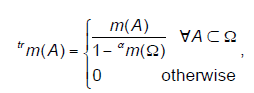 |
| The scenarios associated with this idea can often be found in the multi-evidence pooling systems, where decisions are made based on a set of existing pieces of evidence and the corresponding confidence in (or evaluation of) these pieces of evidence. Evidence and corresponding confidence may be elicited in different manners, e.g., drawn by different experts, or based on different viewpoints. |
PROPOSED FRAUD DETECTION METHOD BASED ON CONTEXTUAL INFORMATION |
| We have chosen the Dempster-Shafer theory for the mathematical representation of the fraudulent behavior - the selling of stolen goods. The theory makes the expression of uncertainty in our model possible. Our uncertainty in the sense that we are not able to say assuredly that certain behavior on certain auction is or is not fraudulent is significant here and we need to express this ignorance, this partial knowledge. Therefore, the Dempster-Shafer theory is particularly suitable for the modeling of evaluation of fraudulent behavior. |
Basics of Our Model |
| Our model consists of four steps: |
| Our model consists of four steps: Step 1. Definition of belief functions representing analyzed fraudulent behavior. In the first step, determinative attributes of fraudulent behavior, the selling of stolen goods, are specified: an inadequately low price mL, goods sold mostly at fixed price mF and variety of goods being sold mV. |
| Step 2. Definition of the reinforcement coefficient on the basis of contextual information. In this step, certain characteristics of contextual information are used to define the reinforcement coefficient α described in Section 3.2. |
| Step 3. Assessment of the influence of contextual information on the evidence about fraudulent behavior. In this third step, contextual information is used to eventually increase the value of the belief function expressing our conviction that stolen goods are sold in analyzed online auction. The aim of this step is to assess the effect of “additional” contextual information about stolen goods. |
| Step 4. Categorization of sellers. In the last step, sellers are categorized according to the resulting belief functions representing the selling of stolen goods into three categories: proper seller, suspect seller and fraudulent seller. |
Definition of Belief Functions Representing Illegal Behavior |
| We explored in detail data about auctions related to five prosecuted cases out of 54 complaints of stolen goods being sold in Internet auctions. Our aim was to determine the characteristics of online auction fraud related to the sale of stolen goods. The cases were the result of complaints lodged with the Czech Trade Inspection (Czech e-shops inspections, 2012). Because detailed judgments were not available for the prosecuted cases, examiners who worked on the cases were interviewed to elicit some additional information. |
| The following attributes of the online auction offering stolen goods were specified: |
| 1. Stolen goods were sold at inadequately low prices (at least about 20% below the price of legitimate goods). |
| 2. Fraudsters prefer to sell stolen goods for a fixed price. |
| 3. A variety of goods were sold via fraudulent accounts (such as car accessories, footwear, sporting goods etc.). |
| 4. Life span of such fraudulent accounts was very short (often less than twelve days). |
| 5. In most cases, the goods were sold within several days of creating the account. In most cases (31 out of 54), the goods were sold within six days of account creation. |
| 6. Fraudsters had accounts on multiple auction systems, and the value of their reputational score is low. |
| Our aim was to define belief functions corresponding to the chosen attributes and then to combine these belief functions to assess whether the respective bidder sells stolen goods or not. Based on our analysis, we have chosen the following attributes as indicators that stolen goods are being sold (the other ones were too difficult to verify or express mathematically): |
| 1. Goods sold at inadequately low prices; |
| 2. Goods sold mostly at fixed prices; |
| 3. A variety of goods being sold. |
| We denoted the frame of discernment concerning the analyzed fraudulent behavior Ω = {stolen, ¬stolen}. Here stolen represents the hypothesis that stolen goods are sold in the analyzed online auction, ¬stolen represents the hypothesis that the analyzed online auction is conducted properly. The power set of the set Ω (the set of all subsets) 2Ω has three elements (we do not consider the empty set here): 2Ω = {{stolen}, {¬stolen}, {stolen, ¬stolen}}, where {stolen, ¬stolen} = Ω denotes our ignorance. That means that we are not able to assess whether stolen goods are sold in the online auction or not. The belief functions expressing our belief concerning single evidences of this fraudulent behavior are described in the next paragraphs. |
| Inadequate low price. This attribute shows that the seller i sells stolen goods for lower prices than the average price of the legitimate goods. The belief functions have the following form: |
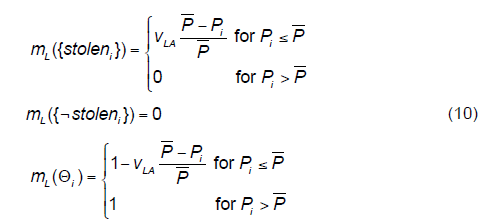 |
| where vL is the weight of this evidence. We can intuitively read this weight as a reliability of this evidence; Pi - is the price at which the seller i sells certain goods. P is the average price of the same goods offered through online auction system. With this equation, we have expressed our belief that the lower the price of goods offered by seller i compared to the average price of respective goods, the higher the suspicion that the seller offers stolen goods. We also assume that the equation reflecting the offering of legitimate goods does not show that the seller does not offer “stolen” goods, i.e mL({¬stoleni}) = 0. |
| Goods sold mostly at fixed price. The sellers (fraudsters) want to sell their stolen goods as quickly as possible. They want to dispose of them quickly and easily. Therefore they prefer to sell the goods at a fixed price (Internet auction systems have the option “buy now”). It is the fastest way to sell goods on an online auction. When a bidder purchases goods at a fixed price, the auction ends, and the seller does not have to wait for the end of the auction. The belief functions have the following forms: |
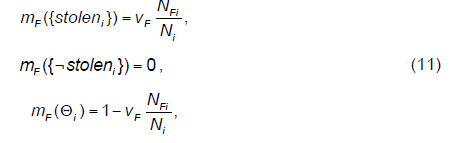 |
| where NFi is the number of goods sold by seller i for the fixed price; Ni is the total number of goods sold by this seller. It is valid that the higher the number of goods sold at fixed price, compared to the total number of goods sold by this seller i, the higher the suspicion that this seller sells “stolen” goods. Therefore, we also assume that the presented equation does not indicate that the seller does not sells stolen goods, i.e. mF({¬stolen}) = 0. The parameter vF is in these equations the weight of evidence. We can intuitively interpret this parameter as the reliability of respective evidence. |
| A variety of goods being sold. Let's suppose that the seller sells stolen goods in online auctions. He sells any kinds of goods that he “gets”. The variety of goods being sold is then higher than that of the average proper seller. The belief functions of this attribute have the following form: |
 |
| where Vi is the amount of different types of goods sold by seller i, and V is the average amount of different types of goods sold by proper sellers in a respective category. The vV parameter is the weight of evidence. We can intuitively interpret this weight as the reliability. It is valid that the higher the variety of goods the seller i sells, compared to the average types of goods sold by proper seller, the higher the suspicion that this seller i sells stolen goods. Therefore, we assume that the given equation does not indicate that the bidder does sell stolen goods, i.e. mV ({¬stoleni}) = 0. |
| Combination of characteristic signs (evidences) of fraudulent behavior. A single characteristic is not enough to identify fraudulent behavior. Thus, once we have obtained more belief functions expressing our belief regarding fraudulent behavior, we combine them in a consistent manner to get a more complete assessment of what the whole group of evidences indicates. The combination of belief functions is done with the help of the Dempster combination rule (4). We express the assumption that a given seller i sells stolen goods with the help of belief function m({stoleni}). We calculate the value m({stoleni}) using the combination of single belief functions expressing appropriate evidence: |
| The operator ⊕ is the Dempster's rule of belief function combination (see equation 4). We perform the combination of multiple evidences according to the Dempster rule first we combine two belief functions, then we combine the result with the third belief function, fourth belief function and so forth. For example, the following rules combine the first and second belief functions: |
| (mL⊕mF)({stoleni})=1/K [mL({stoleni})mF({stoleni})+mL({stoleni})mF(Θ)+mL(Θ)mF({stoleni})], (mL⊕mF )({¬stoleni}) = 1/K [mL(Θ)mE(Θ)], where K = 1- (mL({¬stoleni})mF({stoleni})+mL({stoleni})mF({¬stoleni})). |
| The Definition of the Reinforcement Coefficient α |
| We explored various sources of information on the Internet (on Internet forums, discussions etc.) that could potentially serve as a source of contextual information and could be used to improve the detection of fraud. We extracted pieces of information from these information sources and examined them in detail within the context of online auctions conducted on the Aukro auction portal (Aukro, 2013). For examples, we found complaints discussed in various Internet forums and discussions. For example, some users on these forums complained that somebody had stolen from them a certain object and this object appeared later on an Internet auction. |
| An example is the internet forum (Stolen Columbus, 2011). Here, a user mentions the theft of car navigation device Columbus. At the same forum (Stolen Columbus, 2011), other users inform him that they recently saw this navigation device offered for sale on the Internet auction portal Aukro (Aukro, 2013). Further conversation on this forum relates to whether it could be the stolen device mentioned by the first user. Some users say that it is for certain the stolen device because a) this particular navigation is factoryfitted, b) the price in the online auction is suspiciously low, and c) the online auction in which this device has been sold started few hours after the theft. This case belonged to the five mentioned prosecuted cases from the complaints of selling stolen goods in Internet auctions. |
| We performed further analysis of about 245 different Internet forums and found out that similar conversations occurred in 25 cases which we tried to connect to Internet auctions conducted on the Aukro online auction portal (Aukro, 2013). It is clear that every theft is not mentioned in an Internet forum. However, when we find out information about the theft in Internet forums or discussions, we consider this information as contextual information that can help identify fraudulent behavior - selling stolen goods in the internet auction. |
| We have defined the reinforcement coefficient α as follows: we find out that the stolen object appears in an online auction a short time (some hours) after the theft occurred. The thieves want to dispose of stolen goods as soon as possible. We have expressed the reinforcement coefficient α as a function of time: |
 |
| where K is equal to m(Ω) (see Section 4.2), k is a coefficient that is to be determined on the basis of statistical analysis and t is the difference between the start time of an online auction with goods which have been discussed as stolen on some Internet forum and the time of publication of the complaint on the respective Internet forum. We found out that the person who reports the theft usually provides the approximate time information as well. In the event that the time information about the theft is not specified, the α value is set to α0. The value of α0 is also to be qualified on the basis of statistical evaluations of analyzed auctions. |
| The Assessment of the Influence of Contextual Information on the Evidence about Fraudulent Behavior |
| Let’s suppose that the chosen attributes of an online auction have been examined. The calculated belief assignment m({stoleni}) using the equation 13 of this auction indicates that the seller may be selling a stolen good. At the same time we find out that one of the users of an Internet forum complained that the same good was stolen from him. We consider this information as additional context information that reinforces our belief that stolen goods are sold within this auction. This reflects the fact that part of BBM is transferred from the total frame of discernment m(Ω), denoting our uncertainty, into the element m({stoleni}). This operation reflects our belief related to the sale of stolen goods (we denote this operation as de-discounting or reinforcement, see equations 7 and 8. |
| We can calculate the resulting belief about fraudulent behavior mR(stoleni) by using the equation: |
 |
| We have calculated the belief concerning the certain fraudulent online auction (stolen goods are sold within this auction) mR({stoleni}) with the use of additional contextual information available from Internet sources. This additional information reinforces our confidence that stolen goods are sold within this auction. On the other side, our uncertainty concerning analyzed online auction that stolen goods are sold here will decrease. |
| Categorization of Sellers According to the Resulting Belief Function Representing the Behavior - Selling of Stolen Goods |
| We will divide users into categories according to the degree of belief that a certain user i sells stolen goods, i.e. mR({stoleni}). These categories are: “Proper seller”, “Suspect seller” and “Seller sells stolen goods”. |
| We define two thresholds -η and ξ. The first threshold η is the threshold for determining whether a seller i is a proper seller. If the value of mR({stoleni}) is below η, the seller i will be considered a proper seller. The second threshold ξ is the threshold for determining that a seller i sells stolen goods. If the value of mR({stoleni}) exceeds ξ, the respective seller i will be considered a seller selling stolen goods. If the value of mR({stoleni}) is between η and ξ, we will consider the seller “only” suspect of selling stolen goods. The thresholds η and ξ will be qualified on the basis of statistical evaluations of analyzed auctions. |
| The schema of the proposed model. Major task of our proposed model is to identify sellers who sell stolen goods and identify proper sellers. Figure 1 depicts the schema of our proposed model. |
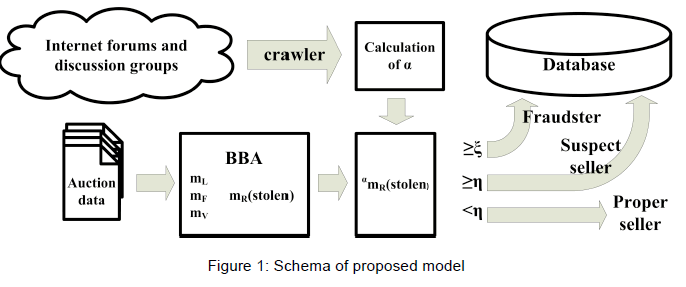 |
| Sellers are evaluated mathematically using a data fusion method that combines information from different information sources on the Internet and auction-level features. The threshold ξ of certifying sellers as Fraudsters, who sells stolen goods, should be fairly high to reduce the number of false positives. |
| For the sellers that are certified as Suspect, the values of their mR({stoleni}) must be lower than ξ but greater than the values of threshold η. This means that the evidence is not sufficient enough to support a conclusion that a seller sells stolen goods, even though the seller behaved more like a fraudster than an honest proper seller. As a result, the seller is considered Suspect. When new additional independent evidence is presented, the Suspect certification will be revalidated. If a seller's certification changes, the new certification is committed to the database. If a seller's certification is labeled as Fraudster, the seller is subject to further investigation and possible punishment, but this fraudster-handling step is outside the scope of this paper. |
CASE STUDY AND ANALYSIS OF RESULTS |
| The motivation for our study was an actual case with which we were familiar: a valuable specific brand-name radio was stolen from a car. The radio owner mentioned the theft including the information about the time of the event on an Internet forum. Others members of this forum reported, as reaction to this information, that an auction selling the same type of radio was taking place at the same time. The radio owner took legal steps then and the perpetrator of the theft was apprehended as the police co-operated with the operator of the online auction portal. Based on the experience from this case, we started a detailed examination of Internet forums and online auctions. We created a simple crawler and searched Czech Internet forums and discussion groups. The aim was to find notices about theft on these forums. Analyses of these notices were performed manually. We performed an analysis of 245 different pages of forums and discussions with the occurrence of words (or their English equivalents) relevant to theft presented in Table 1: |
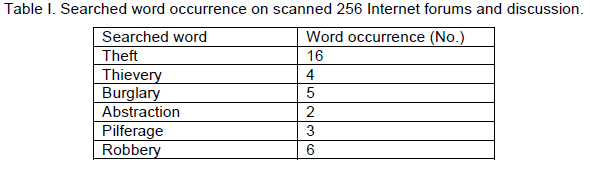 |
| Along with the analysis of Internet forums and discussions, we carried out analyses of online auctions in which objects mentioned on these Internet sources were being sold. We explored bidding history of auctions, prices, goods sold within these auctions and history of seller’s transactions. We had to investigate all information manually because the Czech online auction portal Aukro (Aukro, 2013) does not have (in contrast to eBay) an API interface enabling automatic gathering of information. |
 |
 |
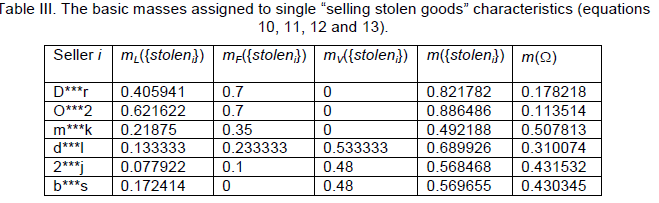
| The values of belief that stolen goods are being sold are calculated using equations 10, 11, 12 and 13. The calculations are presented in Table III. The weights of evidence vL, vF and vV were set in agreement with our experiments at 0.9, 0.7 and 0.8. We consider the character “Inadequate low price” as the most predicative. The character “Goods sold at fixed prices” is the less reliable in determining a seller selling of stolen goods. |
 |
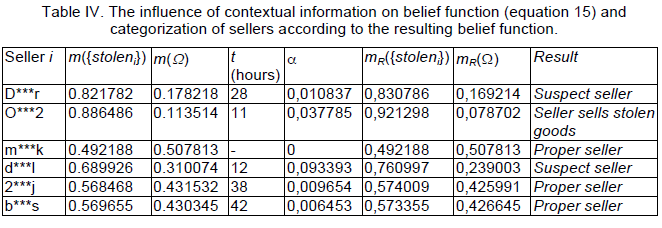 |
| The value t is the difference between the time when the online auction selling goods which have been mentioned as stolen on some Internet forum began and the time of publication of this complaint on the respective Internet forum. The value of k (equation 14) was set on the basis of our experiments at 0.10. The value of threshold ξ was set on the basis of our experiments at 0.90 and the value of threshold η at 0.75. The values α and mR({stoleni}) were calculated using equations 14 and 15. The value mR({stoleni}) expresses our belief that the seller sells stolen goods. On the other side, values mR(Ω) represent our uncertainty or rather ignorance concerning the classification if the seller i sells legal goods or it the seller i sells stolen goods. The values of mR({stoleni}) are high in the case of seller D***r. They are greater than the threshold ξ, hence we consider him/her as seller who sells stolen goods. This seller must then be subject to further investigation. The value of mR({stoleni}) is greater than the threshold η in the case of the sellers d***l and D***r. |
| These sellers are “only” suspected of selling stolen goods. It is recommended to monitor the behavior of these sellers. The values of mR({stoleni}) of the sellers m***k, 2***j and b***s is less than the threshold η. They are considered to be proper sellers. Their behavior on the auction corresponds to the average behavior pattern. |
CONCLUSION AND FUTURE WORK |
| Based on the conceptual framework of Dempster-Shafer theory, a practical approach for detection of a specific type of fraudulent behavior (selling stolen goods) has been proposed. This method in essence takes into consideration evidence found from different information sources, in this case from online auction system and from Internet information sources. Pieces of knowledge about auctions including bidding behavior were processed and quantified. Using the Dempster rule of combination, we combined evidence that enforces each other and resolved the conflicts between different pieces of evidence. We also took into account contextual information from various Internet sources. We consider this information as a factor that can influence (reinforce) our belief concerning the analyzed fraudulent behavior. The case study shows that our proposed approach is quite accurate and practical for real world deployment. |
| We verified our model on the Czech online auction Aukro (Aukro, 2013). We performed a number of experiments on this auction. We made certain that we can increase the detection of fraudulent behavior by using additional information from Internet sources. Nevertheless, we are also aware that the mathematical formalization of parameters used in our model (especially the parameters vL, vF , vV; η and ξ) is necessary to increase the practical usefulness of our model. |
| In our future work, we want to define these parameters with the help of mathematical formulas. We want to perform further statistical analyses of online auctions and Internet sources to verify these formulas and the values of the parameters used in our model. |
| We are convinced that the presented approach represents a promising line of research. Similar methods and systems can be used in particular by auction portals that can monitor suspicious auctions and then provide warnings to users to simply pay attention to what they buy. In addition, law enforcement may use the system to investigate reports of fraud. Substantial limitation is that not all information concerning suspicious behavior on the auctions is available. However, the integration of information from various sources to detection of online fraud is a promising direction for future work. |
References |
|
Copyright © 2025 Research and Reviews, All Rights Reserved