Journal of Internet Banking and Commerce ISSN: 1204-5357
ISSN: 1204-5357
+44-175-271-2024Tochukwu Timothy Okoli
Department of Economics, University of Zululand, South Africa, Private Bag X1001, KwaDlangezwa, 3886, South Africa
Devi Datt Tewari
Professor and Dean of Faculty of Commerce, Administration and Law University of Zululand, Private Bag X1001, KwaDlangezwa, 3886 South Africa
Visit for more related articles at Journal of Internet Banking and Commerce
The rapid global technology revolution has raised serious concerns on what could be its long run impact on banks, especially with its attendant technological unemployment. The on-going debate in literature whether and to what degree financial technology adoption will emit risk to bank profitability is examined in this study. The trade-off analysis and a family of symmetric and asymmetric GARCH approach to Value-at-Risk (VaR-GARCH) based on the camel and value at risk theoretical framework were used to determine potential risk and estimate the conditional variance of bank returns in a panel of thirty-four African countries for the period 2002-2018. The Kupiec log likelihood ratio test and mean relative scaled bias used to evaluate the models’ accuracy and efficiency levels respectively found that the best model to estimate the conditional variance of bank returns is the exponential GARCH (1, 1) with student-t distribution. The worse expected loss on banks’ return due to FinTechs adoption will not exceed 3.01% at 95% confidence interval. Therefore, with a higher FinTechs’ risk/standard-deviations than that of banks’ return and a high VaR value of bank returns, it implies that aside banks, FinTechs also emits risks to other sectors, therefore this study recommends that African economies will benefit from FinTechs diffusion through improved financial service delivery only when a substantial level of collaboration between bank financial institutions and FinTechs companies is reached.
Financial Technology; Banks’ Returns; VaR-GARCH; JEL CODE: G010; G00; C580
Background to the Study
The fact that FinTechs now performs functions which were previously the exclusive reserve of bank financial institutions such a loan extension, fund raising, assets management, payments, credit management, etc. is not only risky to their profitability and continual existence but also to the economy as a whole. With it’s over surging penetration impact in the financial system, the question on how it will affect bank profitability and continual existence has not been empirically addressed.1
The FinTechs revolution accelerated with the new regulations enacted in the wake of the 2008 financial crisis [1-11]. After the 2008 financial crisis, heavy regulations were imposed on the banks, making it much more expensive to extend financial services to their customers. Traditional banks are not only vulnerable to FinTechs penetration in the area of financial service extension but also in assessing the right workforce. The concern on what will be the state of the future financial institutions therefore becomes a researchable issue. Should FinTechs replace the banking sectors or should they collaborate? [9] believes it is not likely that it will replace the conventional banking because, according to them, although FinTechs operations can reduce banks’ profitability, many FinTechs companies actually depends on existing bank accounts. Whatever be the condition, the fact remains that there are potential tradeoffs that is capable of generating both risk and prospects for the bank and the public.
Although the risk potentials of FinTechs are not limited to banks, however, the study concentrates on banks because of the direct involvement of financial technology companies in financial service delivery which used to be the exclusive preserve of banks. Also FinTechs structural transformations transmit risk to the economy at large through its technology unemployment. This is because FinTechs revolution adopts innovated ideas and skills in the area of service delivery thereby making skills completely obsolete, leading to technological unemployment which is capable of reducing the potential growth. Hence, the need to identify the extent of the negative impact of FinTechs on the returns of banks becomes imperative.
With growing uncertainties surrounding the global financial world and the ongoing credit crisis and past financial crisis, it becomes imperative not to only identify the sources of these risks but to also adequately measure it as ‘poor risk measurement can result in bankruptcies and threaten collapses of an entire finance sector’ [12-22]. Therefore, this study aims to ascertain the best risk measurement estimation model that will adequately quantify the loss on banks profitability due to financial technology adoption as well as quantify it.2 However, the argument around this issue is that FinTechs risk encompasses both financial risk/market risk which can be measured whereas technology risk are basically operational risks that involves losses resulting from inadequate or failed internal processes, people and systems, sometimes emanating from external sources [12-27] and they are usually not measurable. Therefore since the aspect of financial technology risk we are interesting to investigate deals with market of banks profitability, we will proceed to quantify it.
Most empirical works on financial risks concentrated on the estimation of markets risks using the VaR model to obtain the value of total worse value of market assets. Apart from the fact that such research dealing on the VaR of assets prices among African economies are limited, the few available ones concentrated on the symmetric GARCH approach to risk measurement with specific country’s analysis. Besides, the short historical time-series data further makes a robust analysis difficult because most stock markets in Africa were established in the early nineties given rise to a more unreliable econometric analysis, especially when VaR approach to risk is applied. More so, as Bucevska [8] observed that only a few of them have tried to consider the effect of a financial crisis on Value-at Risk (VaR) estimation.
Many studies have tried to measure the risk of assets by modeling volatility using the Auto Regressive Conditional Heteroscedasticity (ARCH) approach to VaR model as was developed by Engle [15]. This approach has the ability to capture the characteristic of volatility clustering (ARCH), hence, it has become one of the most popular ways of parameterizing this dependence [16-31]. However, Berggren [5] observed that although symmetric GARCH models presently dominates the volatility estimate of risk using the VaR technique, asymmetric models, such as the exponential GARCH by Nelson [28] and GJR-GARCH by Glosten et al. [17] tend to perform better than the original symmetric GARCH. Similar conclusions were made by Hansen [19,24]. Andersen et al. [1] added that risk management requires multivariate GARCH models such as the EGARCH, due to its ability to accurately forecast volatility. Therefore we hypothesize that asymmetric multivariate GARCH approach to Value at-Risk is a better VaR estimate than the symmetric GARCH models. This hypothesis will be testing in this study3.
Engle [15] argues that we get much better estimates by using models that explicitly allow the standard deviation to change over time (heteroskedasticity). In fact, he suggests two variants, which are the Autoregressive Conditional Heteroskedasticity (ARCH) and Generalized Autoregressive Conditional Heteroskedasticity (GARCH) that provide better forecasts of variance and, by extension, better measures of Value at Risk. Moreover, Berggren [5] affirms that asymmetrical models perform better than symmetrical models. This assertion was consistent with that of Bucevska [8] who tested the relative performance of selected GARCH-type models in terms of their ability of delivering volatility estimates using the daily returns of the Macedonian stock exchange index and found evidence to support Engle [15], moreover, Berggren [5] claim that asymmetric EGARCH model with Student’s t-distribution, the EGARCH model with normal distribution and the GARCH-GJR model are better VaR estimates. Also Brooks [6] in their research on the Southeast Asian stock indices tested the effect of asymmetries on VaR estimation and affirms that the use of asymmetric GARCH in VaR presents a better result while other approaches underestimates the actual risk. The variance and covariance approach to the calculation of Value-at-Risk was adopted by López-Espinosa et al. [26] to identify the main factors behind systemic risk on bank returns and found evidence to support the asymmetries GARCH approach to VaR in capturing the sensitivity of system-wide risk to individual bank returns.
The major weakness of the aforementioned approaches are that those studies tested the relative performances of VaR models at the very beginning of the global financial crisis unlike now that the global financial sector has become very volatile, and on its assumption that the standard-deviation in returns does not change over time (homoscedasticity). Empirical evidences suggest that deviations are not uniform overtime (heteroskedasticity).
Despite the extensive literature and empirical research of estimation of VaR models in the major developed financial markets; the search for the best model is continuously being updated in the literature especially as market risks is being diversified through financial technology adoption. This study intends to adopt different error distribution criteria in a number of symmetric and asymmetric multivariate GARCH to VaR models to estimate the expected short-fall in the profitability of banks that could arise due to FinTechs adoption. To the best of my knowledge, this work has not been done among the Africa economies.
The theories employed in this study are of two basic categories. Firstly, theory that captures the conditional mean model for bank returns is the Camel theory of bank profitability. Secondly, the conditional variance model adopts the use of the symmetric and asymmetric GARCH approach to Value-at-Risk theory to estimate the conditional variance of bank returns/profitability.
The CAMEL Theory of Bank Profitability
The Camel model affirms that bank profitability is a function of their capital adequacy (C), assets quality (A), managerial efficiency (M), earning ability (E) and liquidity (L) of the bank. That is, as long as banks generates a reasonable percentage of their capital to their total assets, keeps its non-performing loan (Assets quality) within a manageable horizon, managerial competency is not compromised, earns good interest on loan (Earnings), and is liquid enough to meet any unforeseen financial obligation without compromising its reserve nor potential investment with high liquidity; they will continue to be profitable. In other words, bank can continually earn profit as long as they maintain a viable confidence of depositors (capital adequacy, measured by the ratio of equity capital to assets); adequately withstands pressures or shocks arising from doubtful loan loss or bad investments (Assets Quality measured by the ratio of non-performing loans to gross loans); management is competent enough to justify the use of assets and/or owners’ equity by lowering cost and raise their profit (measured by the ratio of net profit after tax to assets in the previous period); has sufficient outlets to raise income (measured in terms of noninterest income to total income); and as well as continuously pays its current obligations and meets unexpected withdrawals (Liquidity, measured in terms of bank credit to deposits ratio). Banks with a good standing of this rating will not only be able to generate good returns on assets but will also be able to meet any financial unexpected condition due to Financial risk, credit risk, market risk, interest rate risk and be able to protect the interest of depositors/customers of the bank.
Given these bank profitability measures, this study postulates that with respect to factors that determine banks’ profitability, a potential trade-off exists4. The pairwise correlation result reveals that banks’ profit is more susceptible to managerial competency, liquidity and assets level. Therefore this study considers these measures of profitability as the ratio of banks’ profits to assets (ROAt), managerial efficiency as lag of previous period’s profitability (ROAt-1), bank liquid liability to assets ratio (BLA) and automated teller machine (ATM) to account for bank assets that impacts their profitability in the mean equation.
Value-at-Risk
This is one of the most widely used measures of market risk due to its ability to forecast the worst lost case of a portfolio using a given confidence level over defined period of time. VaR is a gauge that summarizes the worst loss over a target horizon that will not be exceeded with a given level of confidence [29]. It is a statistical measure that estimates potential loss or maximum loss that must not exceed in value of an asset/portfolio, over defined period of time, for a given confidence level. It is a useful measure of market risk therefore can be used to calculate the potential loss arising from financial technology adoption on bank profitability. In other words, VaR can be used to calculate the worst expected loss banks in Africa are disposed to due to financial technology adoption. Value-at-Risk is computationally easy and statistically more accurate given that a better volatility measure of a particular asset is used. In economic literature, ARCH-type models have been used to model VaR [16] and many authors have used the GARCH family models to calculate the Value-at-Risk arising from some portfolio’s risk measure.
The estimation techniques to be employed in this study to quantify the conditional variance and potential losses in banks’ returns are the family of symmetric and asymmetric GARCH approach to Value-at-Risk which includes the symmetric GARCH models, the EGARCH, the GARCH-GJR model and the Asymmetric Power ARCH (APARCH) models. A general finding across studies is that negative returns tend to be followed by periods of greater volatility than positive returns of equal size. In other words, bad news tends to increase volatility more than good news [2]; hence the need for an asymmetric GARCH models.
Following Bucevska [8] and Liu [24], the error term follows three different distributions, which are the normal (Gaussian) distribution, the Student’s t-distribution and the skewed student distribution by Harvey [20]. Furthermore, the researcher subsequently used the model to calculate the Value-at-Risk (VAR) of African’s FinTechs adoption.
Model Specifications: Mean Equation
The conditional mean equation based on theoretical framework is presented thus:
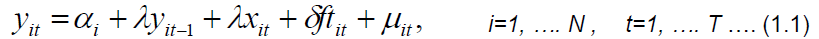
Where yit represents bank profitability (measured in terms of returns to assets ratio),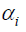
is the intercept, is the ARMA (1, 1) of previous periods’ profitability, a measure of managerial competency, and 
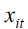is the vector of other determinants of bank profit such as bank liquid liability to assets ratio, while ftit is a measure of bank assets (ATM) that impacts on their profitability and lastly 
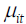is a vector of the independently and identically distributed error terms.
Model Specifications: Volatility/Variance Equations
The conditional variance from equation 1.1 is used to model the symmetric and asymmetric GARCH (1, 1) models. The general form of GARCH (1, 1) is stated thus:
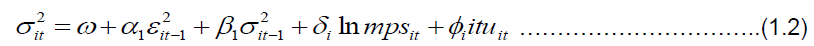
Equation 1.2 is a standard representation of GARCH (1, 1) model in which the first number shows how many autoregressive lags or ARCH terms are in the equation, while the second notation represents the moving average or the GARCH term. The model includes financial technology proxy of log mobile banking (lnmps) and internet banking (ITU) as exogenous disturbances that influence the volatilities in bank returns. As long as α + β < 1, the distant-horizon forecast will be the same for all time periods. Hence the unconditional variance will be mean reverting and conditional heteroskedastic.
The above model (1.2) assumes symmetric effects on volatility. This means that positive and negative information about financial technology should have the same effect on the volatility of banks’ returns. However, empirical evidences suggest that the sign of the error term does matter. Notable among them are Nelson [28], Cheung and Ng [10], Glosten et al. [17]. A general finding across these studies is that negative returns tend to be followed by periods of greater volatility than positive returns of equal size [8]. In order to capture this leverage effect, we adopt models that will consider the asymmetry characteristics of volatility. These include the Exponential GARCH, GJR and the Asymmetric Power ARCH models.
EGARCH: One of the most popular asymmetric ARCH models is the EGARCH model which was developed Nelson [28]. It differs from other GARCH models as it models the logarithm of the conditional variance and includes a multiplicative dummy variable in order to check whether negative shocks are statistically significant. As Nelson [28] noted that negative shocks give rise to larger volatility than positive shocks. The variance equations of EGARCH (1, 1) model can be written thus:
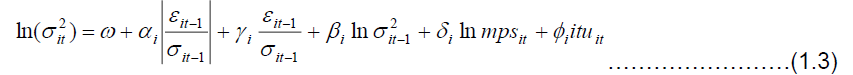
The term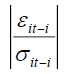 
in the above equation represents the asymmetric effect of shocks. A negative shock leads to higher conditional variance in the following period which is not the case with a positive shock [30]. By testing the hypothesis that 
, we can determine if there is a leverage effect. If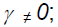 
the impact is asymmetric5. By inclusion of the parameter β in the EGARCH (1,1) model, the persistence of volatility shocks is captured (Bucevska, V. 2012).
GJR-GARCH: Glosten et al. [17] introduced another asymmetric model, the GJRGARCH that takes the sign in front of the return into account. It also takes a multiplicative dummy variable as in the EGARCH. The special form of GJR-GARCH (1,1) is obtained by letting p=r=q=1 and the one-step ahead forecast is expressed thus:
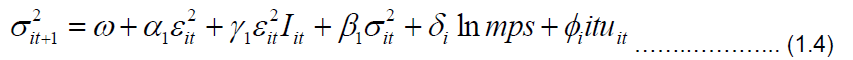
Where α, β and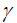 
are constant parameters and I is a dummy variable that takes the value zero (or one) when 
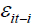is positive (or negative). If 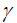is positive, negative errors are leveraged (negative innovations or bad news has a greater impact (α + β + 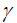)/2 < 1.
APARCH: Finally, the variance equation of the asymmetric power ARCH model, APARCH (p,q) of Ding [12] as stated in (Bucevska, V. 2012) is thus:
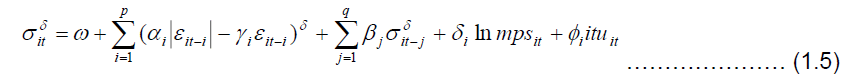
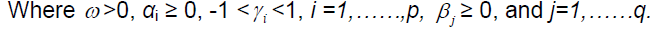
The above models will be estimated using three different error distributions. They are the normal distribution, Student t-distributions and the skewed student distributions. The need for this three distributions were necessary because some authors [15] assumed that returns follow a normal distribution whereas others [6,32] evidenced that standard GARCH models with normal empirical distributions have inferior forecasting performance compared to models that reflect skewness and kurtosis in innovations [8]. Therefore to calculate the VaR arising from the effect of financial technology adoption, the conditional volatility of returns from the variance equations will be multiplied by the quantile of a given probability distribution, e.g. the Normal distribution as shown in the equation below:
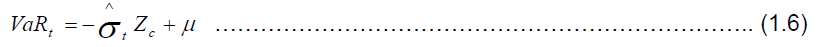
Where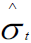 
, is the conditional volatility of returns and Zc stands for the error percentile at c level of significance for the standard normal distribution. Throughout this study, the VaR figures will be given using a 1 % and 5 % significance level, i.e. 1 % and 5 % VaR estimates will be presented. Moreover, the researcher uses the expected short fall or the conditional Value-at-Risk as a coherent measure of risk as the ordinary VaR has been criticized on this ground.
Efficiency and Accuracy Tests to Value-at-Risk Models
The challenge here is in obtaining the best volatility estimation model that will best calibrate the conditional variance as an optimum performance. Engel and Gizycki (1999), proposed two different performance models of volatility estimate as accuracy and efficiency. In this study, we will use the Kupiec Likelihood test of unconditional coverage probability (LRuc) and the expected shortfall (ESF1 and ESF2) to test for the models accuracy whereas for the efficiency test, we will use mean relative scaled bias (MRSB) test6.
Kupiec LR test (KLRT): This test is used to ascertain the sequence or the number of times VaR breaks is violated. That means the number of times the calculated VaR estimate say at 5% for instance exceeds its given horizon due to unforeseen circumstances. It captures reasonable excesses of violations of the VaR estimate. This is otherwise known as Proportion of Failures (POF) as proposed by Kupiec [25]. According to Kupiec [25], the likelihood ratio test for unconditional coverage is used to test the model for accuracy with the null hypothesis that the model is good. The likelihood ratio test statistics is stated thus:
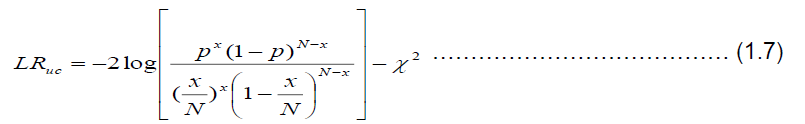
Where x is the number of violations, N is the number of observations in the sample and p is the level of confidence. The LRuc test which is expected to be asymptotically chisquare distribution with [(r-1) (c-1) degrees of freedom where ‘r’ and ‘c’ represents the row and column numbers respectively; to test whether the sample point estimate is statistically consistent with the VaR model's prescribed level of confidence. The null hypothesis that the model is good is rejected if the LRuc statistics is greater than the critical value of the chi-square distribution (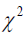
) at 5% level of significance, otherwise accept the null hypothesis. If we reject the null hypothesis, it means that the model is inaccurate therefore; it is either underestimating or overestimating the risk.
Expected shortfall and tail measurement: Given that value-at-risk may give an under approximation of potential loss values because it ignores all losses worse than the given VaR level, however, the expected shortfall incorporates this by giving us the average potential losses beyond the given VaR7. Therefore, Value-at-Risk measure of risk is a less coherent measure of risk [4]. It tends to ignore the average loss beyond the VaR quantile level. The expected short fall therefore is found to be more coherent measure of risk because it considers the average loss beyond the VaR quantile; hence it’s otherwise called the conditional value-at-risk. As the name implies, it represents the expected value of losses conditional on the loss being larger than the VaR. It is often categorized as ESF1 and ESF2. The former is the expected amount of loss beyond VaR level, whereas the latter is the same expected value of loss beyond VaR divided by the value of VaR [21].
Mean relative scaled bias (MRSB): VaR accuracy yard-stick for ascertaining whether or not a VaR model is good or not is very useful, however, efficiency looks at how best the parameters are free from bias and were better estimated. This study employs the MRSB approach proposed by Hendricks [21] to measure the models’ efficiency. The most efficient model is the one with the least average risk bias or the least MRSB value. This we can do by comparing the scaled VaR numbers with their relative average sizes by using the following calculation:
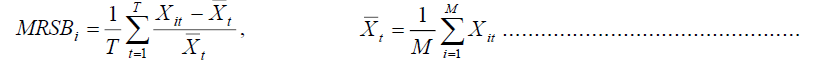(1.8)
Where T is the number of computing years of one period ahead VaR, M is the number of VaR models to be estimated whereas Xit is the returns or the volatility.
Data Sources and Scope of the Study
In this section, we presented the scope, data and their various measurements as well as discuss some of their peculiar properties. The data used includes Bank profits to assets ratio, bank liquid liability, Automated Teller Machine (ATM), log of mobile phone subscription, internet users to total population and they were sourced from the World- Bank database for the period 2002 to 2018. The study covers thirty-four African economies (see the countries under the Appendix). The choice of thirty-four countries was necessary to have a large data series required for the conditional volatility to converge (Figure 1).
Figure 1: Descriptive statistics.
Preliminary Analyses
Three basic preliminary analyses were estimated to see the inherent statistical properties of the data. They include the descriptive statistics, correlation matrix and
The descriptive statistics: The descriptive statistics as presented in Table 1 shows the four basic moments (mean, standard deviation, skewness and kurtosis) of the distribution. The result reveals that all the series reported positive annual mean values over the sample period of five hundred and seventy eight years. The statistics reveals that bank returns averaged about 2.07% with a standard deviation of 1.42%. This suggests that the riskiness of banks’ returns is very low, hence might not be too vulnerable to financial technology diffusion. In the same vain, the standard deviations of financial technologies ATM (14.39299), internet banking (13.61323) and mobile banking (1.878175) is very high, signifying that they are very risk. Also the negative skewness for mobile banking implies that negative effects of financial technology are leveraged or are asymmetrical, which is a deviation from normality of returns. Therefore, their combined effect on the conditional variance of bank returns might be high, thereby reporting a higher Value-at-Risk.
| AFRICAN COUNTRIES | ||||||
|---|---|---|---|---|---|---|
| Algeria | Burundi | Ethiopia | Malawi | Namibia | Sierra Leone | Tanzania |
| Angola | Chad | Gabon | Mali | Niger | Seychelles | Togo |
| Benin | Cameroon | Ghana | Mauritius | Nigeria | South Africa | Tunisia |
| Botswana | Cote d’Ivore | Kenya | Morocco | Rwanda | Sudan | Zambia |
| Burkina Faso | Egypt | Madagascar | Mozambique | Senegal | Swaziland | |
Table 1: African Countries Specification.
The mean and median can be used to determine the skewness of the distribution. A distribution is said to be symmetrical or has zero skewness if the mean and median are equal. From Table 1, we can see that the mean and median value for lnMPS is almost equal, hence implying symmetrical condition. This was also confirmed by the skewness value which is almost zero. Also, the residuals from the mean equation 1.1 reveals that banks’ returns have evidence of fat tails, since the kurtosis exceeds the normal value of three (3) therefore they are leptokurtic while positive skewness on the other hand reveals that the right tail is particularly extreme. This implies that there is an asymmetric effect in the series, thereby strengthening the use of the asymmetric GARCH models to estimation the model. The Jarque-Bera test of normality is a test of the joint hypothesis that skewness and kurtosis are 0 and 3 respectively [18]. Kurtosis measures the degree of flatness of a symmetry distribution compared with a normal distribution of the same variance. The Jarque-Bera probability for the variables shows that the error terms are not normally distributed.
The pairwise correlation matrix: On the other hand, the pairwise correlation matrix was used to ascertain whether there is any potential trade-off between financial technology proxies and bank returns. A significant trade-off implies that financial technology adoption will detract potentially on the ability of banks to raise profit. The result as presented in Table 2 under the appendix shows that trade-off exists. Therefore, financial technology adoptions among African economies are done at the risk of bank profitability. Take for instance, a one unit rise in internet banking (ITU) will significantly reduce bank profits by 13.04 percent, all things being equal.
| GdpGR | ROA | ATM | BLA | ITU | LnMPS | |
|---|---|---|---|---|---|---|
| GdpGR | 1.0000 | |||||
| ROA | 0.1514 | 1.0000 | ||||
| ATM | -0.1416 | -0.0041 | 1.0000 | |||
| BLA | 0.0130 | -0.0969 | -0.1527 | 1.0000 | ||
| ITU | -0.1657 | -0.1304 | 0.6969 | -0.0832 | 1.0000 | |
| LnMPS | -0.0345 | -0.1945 | 0.0702 | 0.1492 | 0.3083 | 1.0000 |
Source: Estimation
Table 2: Pairwise correlation of the Distribution, Star (5% sig.)
The ARCH test: Further analyses were conducted to verify the best model to use. Therefore in order to verify whether there is serial correlation in our data set, Arch effect and to see if there is clustering volatility in our data set, we present the residuals from the mean equation 1.1 in Figure 2 as well as the autocorrelation functions. The presence of ARCH effect and clustering volatility will justify the adoption of a family of symmetric and asymmetric GARCH to estimate the Value-at-Risk arising from financial technology on the profitability of commercial banks.
Figure 2: shows the line graph of African economies’ bank returns to assets ratio in panel A and the residuals from the mean equation 1.1 in panel B. The series suggest evidence of clustering volatility among the residuals; periods of low volatility was followed by periods of low volatility and periods of high volatility was also followed by periods of high volatility.
Moreover, the residual shows that there are periods of large fluctuations which suggest that there might be the presence of ARCH effect in the residual series. Moreover, the residual was tested for auto correlation in the squared residuals as presented in Figure 3. From the correlogram table below, we can detect the presence of ARCH effect and significant serial correlations in the series of order one. This justifies the inclusion of an autoregressive term in the conditional mean equation 1.1 above8. On the detection of serial correlation in the residuals, the researchers can remove it by fitting ARMA (p, q) and the GARCH models [33,34]. Note that the presence of serial correlation was detected with the strong significance of the p-values from the correlogram table.
Figure 3: Residual Correlogram from mean equation. Sources:
Since we have ascertained that there is presence of ARCH effects, clustering volatility and autocorrelation of order one in the residuals derived from the mean equation of model 1.1, we proceed to estimate the models. After estimating the models, we can conduct the ARCH-LM test by Engle (1982) to detect if there is the presence of ARCH effects in the residuals to justify or debunk the use of the GARCH models whether they successfully capture the persistence of volatility shocks.
The mean and variance equations results were presented in Tables 3 and 4 under the appendix. The mean equation with bank returns as the dependent variable follows the theoretical framework to model an ARMA (1) model, while bank liquid liability to assets ratio (BLA) and ATM constitutes the explanatory variables. The variance equations include the external disturbances of FinTechs proxy as log of mobile banking (lnmps) and internet banking. The assumption here is that financial technology adoption detracts from the returns of banks; therefore the prior expectation is that they will be negatively significant (Table 5).
| GARCH (1,1) | EGARCH (1,1) | |||||
|---|---|---|---|---|---|---|
| MODEL 1 | MODEL 2 | MODEL 3 | MODEL 4 | MODEL 5 | MODEL 7 | |
| Normal Dist. | Student-t Dist. | Skewed Std-t | Normal Dist. | Student-t Dist. | Skewed Std-t | |
| CSt (M) | 0.4764 c | 0.4249 a | 0.4540 a | NA | NA | NA |
| Lag ROA | 0.7487 a | 0.7758 a | 0.7726 a | 0.8637 a | 0.8937 a | 0.8984 a |
| ATM | -0.0006 | -0.0017 | -0.0019 | -0.0036 c | -0.0039 a | -0.0033 a |
| BLA | -0.0001 | 0.00001 | 0.0001 | 0.0039 a | 0.0042b | 0.0035 a |
| Cst(V) ω | NA | 3.6280 a | 3.6105 a | NA | NA | NA |
| ARCH (αi)(-1) | 0.6940 c | 0.4603b | 0.4197b | 0.3711 | -0.5958b | -0.9314 a |
| GARCH (βi)(-1) | 0.4273 a | -0.0479 | -0.0553 | 0.5968 a | 0.8684 a | 1.0003 a |
| γ1 (Gammal 1) | NA | NA | 0.0754 | -0.124 | -0.055 | -0.144 |
| γ2 (Gammal 2) | NA | NA | NA | 0.746 a | 0.858 a | 1.275 a |
| δ (lnMPS) | 0.0181 a | -0.1760 a | -0.1751 a | 0.0447b | 0.0225 | -0.2947 a |
| ÃÂÃ⢠(ITU) | -0.0046 | -0.0070 a | -0.0070 a | -0.0393 a | -0.0364 a | -0.0264 a |
| α + β | 1.1213 | 0.4124 | 0.3644 | NA | NA | NA |
| MRSB | -0.001137 | 0.000782 | -0.001058 | 0.000248 | -0.00518 | 0.0032983 |
Note: a, b and c denotes significance level at 1%, 5% and 10% respectively
Source: Authors’ Estimation.
Table 3: Symmetric and Asymmetric Volatility Models on Bank Returns
| Models | GJR-GARCH (1,1) | APARCH (1,1) | |||
|---|---|---|---|---|---|
| MODEL 8 | MODEL 9 | MODEL 10 | MODEL 11 | MODEL 12 | |
| Distributions | Normal Dist. | Student-t Dist. | Skewed Std-t Dist. | Normal Dist. | Student-t Dist. |
| CSt (M) | 0.4518b | 0.4267 a | 0.4678 a | 0.5471b | 0.4428 a |
| Lag ROA | 0.7471 a | 0.7757 a | 0.7710 a | 0.7450 a | 0.7791 a |
| ATM | -0.0005 | -0.0017 | -0.0019 | -0.0038 | -0.0025 |
| BLA | 0.0001 | -0.000001 | 0.0001 | -0.0005 | -0.0003 |
| Cst (V) ω | NA | 3.6425 a | 3.63 a | 4.0469 a | 4.1731 a |
| ARCH (αi)(-1) | 0.5955 c | 0.4830b | 0.5012b | 0.3047 a | 0.3250 a |
| GARCH (βi)(-1) | 0.4213 a | -0.0482 | -0.0504 | -0.6940 a | -0.5794 a |
| γ (Gammal) | 0.2295 | -0.0534 | -0.1956 | -0.0474 | -0.0262 |
| δ (lnMPS) | 0.0189 a | -0.1769 a | -0.1765 a | -0.1633 a | -0.1795 a |
| ÃÂÃ⢠(ITU) | -0.0050 | -0.0070 a | -0.0068 a | -0.0119b | -0.0089 a |
| MRSB | -1.97E-06 | 0.000157 | 0.005838 | -0.000725 | -0.001159 |
| Note: a, b and c denotes significance level at 1%, 5% and 10% respectively | |||||
Source: Authors’ Estimation.
Table 4: Asymmetric Volatility Models on Bank Returns
| MODELS | Dependent V. | Quantile | KLRT | P-Value | ESF1 | ESF2 | VAR |
|---|---|---|---|---|---|---|---|
| GARCH-ND | ROA | 0.95 | 0.0886 | 0.766 | 5.0047 | 1.3835 | 3.62% |
| 0.99 | 5.2032 | 0.0225 | 6.3539 | 1.4336 | 4.43% | ||
| GARCH-SD | ROA | 0.95 | 0.4998 | 0.4796 | 4.7489 | 1.3878 | 3.42% |
| 0.99 | 0.1554 | 0.6934 | 7.8875 | 1.5567 | 5.07% | ||
| GARCH-SSD | ROA | 0.95 | 0.0124 | 0.9112 | 4.9073 | 1.3964 | 3.51% |
| 0.99 | 0.1554 | 0.6934 | 7.8875 | 1.4931 | 5.28% | ||
| EGARCH-ND | ROA | 0.95 | 0.8119 | 0.3676 | 4.4347 | 1.3238 | 3.35% |
| 0.99 | 10.668 | 0.0011 | 5.4503 | 1.3231 | 4.12% | ||
| EGARCH-SD | ROA | 0.95 | 4.1017 | 0.0428 | 4.2986 | 1.4289 | 3.01% |
| 0.99 | 1.4315 | 0.2315 | 6.4228 | 1.637 | 3.92% | ||
| EGARCH-SSD | ROA | 0.95 | 1.6464 | 0.1995 | 4.4165 | 1.3055 | 3.38% |
| 0.99 | 0.1554 | 0.6934 | 6.9092 | 1.3017 | 5.31% | ||
| GJR-GARCH-ND | ROA | 0.95 | 0.2562 | 0.6127 | 5.0823 | 1.4025 | 3.62% |
| 0.99 | 6.8583 | 0.0088 | 6.0761 | 1.3946 | 4.36% | ||
| GJR-GARCH-SD | ROA | 0.95 | 0.4998 | 0.4796 | 4.7489 | 1.3902 | 3.42% |
| 0.99 | 0.6481 | 0.4208 | 7.1764 | 1.4824 | 4.84% | ||
| GJR-GARCH-SSD | ROA | 0.95 | 0.0124 | 0.9112 | 4.8538 | 1.3968 | 3.47% |
| 0.99 | 0.0016 | 0.9679 | 8.229 | 1.5972 | 5.15% | ||
| APARCH-ND | ROA | 0.95 | 0.8687 | 0.3513 | 5.0621 | 1.33 | 3.81% |
| 0.99 | 6.8583 | 0.0088 | 5.6978 | 1.2486 | 4.56% | ||
| APARCH-SD | ROA | 0.95 | 0.0975 | 0.7548 | 4.8157 | 1.3381 | 3.60% |
| 0.99 | 0.1554 | 0.6934 | 7.3425 | 1.4042 | 5.23% |
Source: Authors’ Estimation
Table 5: Value-at-risk and expected shortfall table.
The variance equation comprises of one symmetric (GARCH (1, 1)) model and three asymmetric models (EGARCH, GJR-GARCH and APARCH) with three different distributions as normal, Student-t and Skewed student-t distributions. This is necessary for robustness check. Given that we have four models with three different distributions, we therefore present a total of twelve estimates, except for the ROA skewed student-t distribution that couldn’t reach convergence. The accuracy/validity and efficiency of the models were performed using the Kupiec LR test (KLRT) and the mean scaled relative bias respectively as discussed above. The model is found to be accurate if the number of exceedances is close to the number implies by VaR quantile or if the Kupiec LR test is less than their respective critical values of chi-square (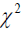 
) at [(r-1)(c-1)] degree of freedom, where ‘r’ is the number of rows (17) and ‘c’ is the number of columns (3). Therefore their results show that the asymmetric EGARCH (1, 1) model with student-t distribution performs better in fitting the volatility clustering arising from FinTechs to the returns of banks among African economies because the Kupiec LR value (4.10) is less than the critical value (46.19) of chi-square ( 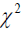) at 32 degrees of freedom. Moreover, the model is found efficient because the Mean Relative Scaled Bias (MRSB) for the asymmetric EGARCH (1, 1) was least compared to other models. These indicate that the VaR quantile of 95% are largely well calibrated, hence, the number of times the calculated VaR estimate at 5% exceeds its given horizon due to unforeseen circumstances were not statistically significant, and that the parameters are free from bias, therefore they were better estimated under asymmetric EGARCH (1, 1) with student-t distribution for bank returns.
The ARCH and GARCH effects for most of the models were found to be statistically significant, particularly under model (5)9 which is our model of interest. This model, EGARCH (1, 1) with students’t-distributions reveals that both the ARCH and the GARCH effects were significant in explaining the volatility of bank returns. In other words, the previous period’s squared returns or previous period’s information about the returns of banks (ARCH) and the previous period’s volatility (GARCH) affect impacts on the current day’s volatility of banks’ returns. However, whereas the ARCH effect dampens it, the GARCH effect increases it. The asymmetric coefficient (γ2=0.858)10 of the model was statistically significant, suggesting that negative information, especially as regards the effect of financial technology on bank performance is leveraged. It has serious impact on the volatility of banks’ returns than positive information among African economies. According to Angabini and Wasiuzzaman [2] the exponential nature of the EGARCH model guarantees that the conditional variance is always positive even if the coefficients are negative, hence a justification for its positive coefficient. The model’s stability was tested using the behavior of alpha (α) and beta (β). The result found that the persistence of the conditional volatility decays fast overtime because their sum (0.2726) is less than positive unity, and is closer to zero than to one, that is α + β < 1. This finding is consistent with the established behavior of financial assets in the literature, such as Bucevska [8] who asserts that by the inclusion of the parameter β in the EGARCH (1, 1) model, the persistence of volatility shocks is captured.
Another main finding from the result estimate is that delta (δ) and phi (ÃÂÃâ¢), the coefficients of mobile banking (lnMPS) and internet banking (ITU) respectively in the variance equations impacts on the volatility of banks’ returns differently. Whereas mobile banking could not significantly explain the volatility on banks’ returns, internet banking was negatively significant as well as in almost all the models. This implies that financial technology/internet banking is an aspect of risk to banks’ returns. This assertion is supported by the ways financial technology extends financial services through encrypted technologies which were primarily the sole responsibility of bank financial institutions. Hence, banks’ ability to raise profits through loan extension is now being restricted. Moreover, the structural and sophisticated nature of financial technology displaces people from their jobs especially in the banking industry. These two effects can dampen the banks’ profits at least during the short run.
This study empirically examined the value-at-risk (VaR) on banks’ returns due to financial technology adoption in Africa. The general background and the rationale of the study hinges on the ongoing debate in economics and financial literatures on whether financial technology will culminate into potential risk to bank profitability, especially in the long-run. This chapter empirically settled for the affirmative that yes financial technology imposes some measures of risk on banks’ profit through its trade-off analytical and asymmetric GARCH results.
The mean equation model specification was based on the camel theoretical framework. Bank profits to asset ratio was used to measure the banks’ returns while the methodology employed a family of symmetric and asymmetric GARCH approach to value-at-risk to estimate the volatility of banks’ returns. Moreover, the variance equations included the exogenous disturbances of financial technology as log of mobile banking (lnMPS) and internet banking (ITU) and found evidence that whereas the former does not significantly detract from banks’ profitability, the latter has a potential risk impact on it. The residual calibration follows three different error distributions which are normal, student-t and skewed student distributions. This was necessary to have a more robust and reliable parameter estimates, and two basic evaluation criteria of Kupiec log likelihood ratio test and mean relative scaled bias were used to test the models’ accuracy and efficiency levels respectively. Their findings reveals that the best model for the estimation of the conditional variance of bank returns is the exponential GARCH (1, 1) model with student-t distribution because the number of times the calculated VaR estimate at 5% exceeds its given horizon due to unforeseen circumstances were not statistically significant. In other words, the Kupiec log likelihood ratio value for the model was less than its critical value at 5% significant level; moreover the parameters are free from bias.
The worse loss value that banks are expected to lose due to FinTechs adoption from the selected model (5) will not exceed 3.01% and 3.92% at 95% and 99% confidence levels respectively11. The fact that the riskiness/standard deviations of financial technology are quite large, while the estimated VaR value on the volatility of banks’ returns is relatively low, this study therefore concludes that the implication of this is that FinTechs also emits risks to other sectors of the economy other than the banking sector with a high future risk propensity to banks. Therefore given the above results and conclusions, this study recommends that African economies will benefit from FinTechs diffusion only when a substantial level of collaboration between bank financial institutions and FinTechs’ companies is reached.
1 The research question here is: Is there a potential short-fall on bank returns arising from FinTechs’ adoption?
2This is the main objective of this study
3This hypothesis is tested using the mean relative bias (MRSB) model evaluation technique; with a lower MRSB of the asymmetric EGARCH (1, 1) model, we settle for the null hypothesis that the asymmetric EGARCH (1, 1) model is a better risk estimation model than the symmetric GARCH (1, 1) model.
4By this, we mean that while a good standing of this variables can spur higher profit, a rise in one can worsen another thereby reducing entire profit. In a nutshell, multicollinearity among the regressors can be a major issue in bank profit determinants hence the need to drop some highly correlated explanatory variables. This was done using the pairwise correlation analytical technique and having dropped the correlated variables, we are left with only three major explanatory variables for the mean equation.
5The leverage effect was tested for the best Var calibrated EGARCH model estimate based on the evaluation criterion of MRSB and Kupiec log likelihood ratio, and found that the null hypothesis of no asymmetric effect is rejected because the leverage coefficient (γ2) is=0.858 ≠ 0. Therefore the model is mean reverting.
6The results of the Kupiec log likelihood ratio used to ascertain the number of times VaR breaks is violated is presented under table 1.4A under the appendix whereas the result of the Mean Relative Scaled Bias (MRSB) used to test the models’ efficiency is presented in tables 1.3A and 1.3B still under the appendix.
7This result is presented in table 1.4A under the appendix.
8The residual and the correlogram suggest the use of an Autoregressive of order one in our mean equation, hence the use of the first lag of the dependent variable in the mean equation (1.1) above.
10See table 1.3A under the appendix in model 5 for the asymmetric effect.
Copyright © 2024 Research and Reviews, All Rights Reserved