ISSN: 1204-5357

Reach Us +44-175-271-2024
All submissions of the EM system will be redirected to Online Manuscript Submission System. Authors are requested to submit articles directly to Online Manuscript Submission System of respective journal.

Credit Risk Prediction to Individuals

LYUDMILA VYACHESLAVOVNA EFIMENKO South Ural State University (National Research University), 76 Lenin prospekt, Chelyabinsk, 454080, Russian Federation, Tel: +7(351)452-13-25 Email: yelusia@yandex.ru
TATYANA ALEKSANDROVNA SHINDINA South Ural State University (National Research University), 76 Lenin prospekt, Chelyabinsk, 454080, Russian Federation
ELENA VASILEVNA TABAKOVA South Ural State University (National Research University), 76 Lenin prospekt, Chelyabinsk, 454080, Russian Federation
ALEXANDRA VITALEVNA GAVRILOVA South Ural State University (National Research University), 76 Lenin prospekt, Chelyabinsk, 454080, Russian Federation
*Corresponding Author: LYUDMILA VYACHESLAVOVNA EFIMENKO, South Ural State University (National Research University), 76 Lenin prospekt, Chelyabinsk, 454080, Russian Federation, Tel: +7(351)452-13-25, Email: efimenko407930@mail.ru

Visit for more related articles at Journal of Internet Banking and Commerce

Abstract

Loans to individuals become the most vulnerable segment of commercial banks’ investment in a volatile financial environment. Searching safe methods for modelling refund loans reliability is one of the methods for credit losses risk reduction in commercial banks. In this article, such problems as a credit risk increase and an effective means of its evaluating are considered. In addition, it is proposed to solve these problems by developing a mathematical model describing dependence between loan defaults and the factors characterizing the financial reliability of the borrower through the credit transactions example with individuals of a particular bank. The purpose of this model is to identify the relationship between the independent variables. The development of regression models to estimate losses from repayment risk from individuals is described in this article. The model reflects the relationship between significant independent factors characterizing the degree of the borrower’s financial reliability according to the component analysis method based on the model of David Cox.

Keywords
Principal Component Method; Regression Model; Repayment Risk; The Financial Reliability of Borrowers

INTRODUCTION
The globalization of banking system, sharpening competition between financial institutions are the reasons to study the problems of banking system stability and developing a monitoring risks system and providing effective credit risk management of commercial banks.
In the modern economy, the actual problem of commercial banks is the growth of loan default from individuals caused by deepening financial crisis and effective demand decrease of the population [1,2]. The crisis in global and domestic monetary markets confirmed the necessity of improving assessment of the financial strength of borrowers and monitoring of proactive risk level in the banking sector. It is necessary to manage risks taking into account that they are correlated and risks reduction depends on factors decreasing probability of negative consequences [3]. Organizing effective management risk system depends on correct evaluation of risks. This assessment should be considered when building individual (differentiated) relations with customers taking into account not only capacity to pay debt but also the duration of interaction with them [4].

METHOD
Development of regression model for predicting financial strength of borrowers, which based on the method of principal components [5].
The main point of principal components method is tracking the qualitative characteristics’ impact of potential borrowers of a commercial Bank on the non-payment risk of loan contract. This method includes the following steps:
1. Forming the set of target and underlying factors that assess changes in the credit portfolio of Bank customers with regard to their financial reliability.
2. The choice of target factors and formulation of requirements to the model of credit risk management under contracts with individuals (models for predicting the financial reliability of customers).
3. The decomposition of set of key indicators into several groups, assessing the most important socio-demographic characteristics of borrowers that affect their creditworthiness, their own the financial risks of the creditor (principal components). Calculation of principal components and principal factors, the choice of key indicators and ranking factors.
4. Principal component analysis for compliance with requirements to financial reliability model of customers.
5. The evaluation of management efficiency of credit resources for the variances of principal components that meet the requirements of the model.

Choice of Factor Index of the Model
When making any type of loan, each creditor always conducts a credit analysis. As a rule, for the analysis we can use several methods to calculate the reliability of the borrower, including the scoring programs of assessment borrower’s creditworthiness. This assessment takes into account financial risks of the Bank, so chosen criteria and the methods of quantitative estimation for each creditor are individual and depend on changes of the credit policy at some stage. Although there is no standard of credit assessment, banks choose almost the same criteria. Each Bank develops its own scoring model, which includes such criteria as credit history of the applicant, job title, marital status and others.
According to the authors, scoring evaluation of creditworthiness of the borrower is not reliable to identify the risk of non-payments under concluded contracts. However, criteria indicators used for scoring are suitable for developing new approaches in predicting the risk of defaults on loans to individuals.
A standard tool for forecasting is regression analysis as regression models can explain the behavior of dependent factors under the influence of variables’ combination according to their importance [6,7].
Managing credit risk, we should develop a mathematical model that allows determining correlation between borrowers’ behavior and independent factors. The next step is to choose the main independent factors ones so that calculated indicators are maximum close to exist transactions’ loss of a commercial Bank.
Regression analysis helps to determine different factors’ influence on loan repayment from individuals to LLC "Russian finance Bank". Nowadays the Bank uses a scoring method of evaluating the borrowers’ credit worthiness to reduce credit risks. Experts of Bank point out the following main parameters for this analysis: the borrower's age, the marital status, a number of dependents, a scope of activities, qualifications, work experience and monthly income [8] that can be used as variables and evaluated according with rating evaluation scale. Experts know or guess which factors could be significant. The factors that are interesting for the analysis, can be called target factors. Bank experts focused on the personal data of borrowers choosing classification criteria. Creditworthiness of borrowers is borrowers’ ability to fulfill their obligations [9]. In our view, the term “financial reliability” of the borrower is more suitable for individuals, describing their intentions regarding compliance with terms of the loan agreement [10].
Factor indicators proposed to assess the level of financial reliability of a borrower and their value of data point; they are in Table 1.

Features of Regression Models Development Based on Principal Component Analysis
To predict the risk of non-payment we use the method of principal components. It allows to reflect complex problems and tendencies of development of the lending processes in a simplified form using mathematical model and studying possible varients of their development [5].
At first, there is hypothesis about the variable depends on the set of endogenous (independent) variables and then regression model is being developed (formula 1):
Y=α1 x1+ α2 x2+… αn xn+ ε,          (1)
where α – the vector of unknown coefficients, y – the vector of m observations of the dependent variable, measured about its mean value, x – a matrix (m x n) of independent variables, also measured relative to their average values, x – a matrix, each column of which contains all the values of one independent variable, ε – a vector of errors.
Regression analysis is for testing the statistical significance of the model with this hypothesis. Regression analysis does not “prove” a hypothesis but confirms or disproves. Principal component regression is a regression analysis that uses principal factors obtained in the calculation of “principal component of a set of endogenous variables”, instead of “themselves endogenous variables.”As the main components are uncorrelated, so there is no multicollinearity between them, and the values of regression coefficients are more numerically stable to multicollinearity of endogenous variables [11].

The Basic Data and the Algorithm for Constructing Regression Models Based on Principal Component Analysis
The first step is to determine the main (important) features (independent variables) that are factor indicators presented in Table 1. For forecasting potential losses due to credit default, we can use a "Cox’s proportional risk model" [12], which describes the dependent variable as an exponential function by the formula (2):
Y=e(α0+ α1 x1+ α2 x2+ α3 x3+ α4 x4+ α5 x5+ α6 x6+ α7 x7)            (2)
wherex1 – borrower’s age;
x2 – marital status;
x3 – number of dependents;
x4 – scope of activities;
x5 – qualifications;
x6 – work experience;
x7 – monthly income;
y – repayment risk.
The argument of the function is a linear combination of the covariance. Thus, the Cox model is the dependence of function of defaults in a certain time (in our case, this time is the expiration of the contract) in the form of two factors:
• basic intensity function that reflects some natural level of losses that does not depend on independent variables;
• values of the loss function, explained by the covariance. (the covariance is a variable that can affect the relationship between the studied variables).
The basic function of the intensity coincides with the evaluation of loss functions in case of absence of the influence of all independent variables in the model. Cox’s proportional risk model can be traced to a linear relationship, taking the logarithm at both sides of the equation in the model, and then we get an equation of the following form:
lny=ln(e(α0+ α1 x1+ α2 x2+ α3 x3+ α4 x4+ α5 x5+ α6 x6+ α7 x7)),
lny= α0+ α1 x1+ α2 x2+ α3 x3+ α4 x4+ α5 x5+ α6 x6+ α7 x7
elny= e(α0+ α1 x1+ α2 x2+ α3 x3+ α4 x4+ α5 x5+ α6 x6+ α7 x7)
The choice of independent factors influences on the studied index made according to qualitative and quantitative analysis of the investigated characteristic. At first, covariance matrix of independent characteristic is formed, and then target factors-characteristics are selected to develop regression model
For the regression analysis, we use a sample of loans to borrowers that vary in social and business characteristics. The sample contains the values of the 8 indicators for 72 borrowers. The list and the values of the basic factors-characteristics on borrowers with a different set of social and business characteristics are in Table 2.
We use classical regression analysis with the method of principal components for developing the model where independent variables are basic indicators. When using method of principal components, principal components are used as independent variables [5,11]. Retrieving data from a General population is based on internal reporting of a commercial bank of the Chelyabinsk region (LLC “Rusfinance Bank”) during the full period of execution of the loan agreements. To construct the model we use data for the first 60 borrowers (empirical sample), the data of the last 12 borrowers is for evaluating the accuracy of prediction (test sample).
Table 3 shows the values of regression coefficients and significance coefficients of the regression model factors.
Regression analysis examines the statistical consistency of the model with this hypothesis. Regression analysis does not “prove” a hypothesis; but only confirm or refute. Principal component regression is a regression analysis that uses principal factors obtained in the calculation of “principal component of a set of endogenous variables”, instead of “endogenous variables”. As the principal components are uncorrelated, there is no multicollinearity between them, and the values of regression coefficients are more numerically stable to multicollinearity endogenous variables. The influence of principal components on the dynamics of target factors falls sharply with the increase of the number of the main components if their eigenvalues are numerically equal to the variance of the respective main factors. The most important are the first five or six principal components. Thus, changing target factors of model to predict the financial reliability of customers with a very high accuracy can be described by the first five principal components. Accordingly, when analyzing the model of financial reliability, we can choose the set of the first five components [13].
The calculation of principal components allows identifying the most and least significant components. Therefore, we use the program “MIDAS” to calculate characteristic vector, defined for a square matrix or a vector that is multiplied by a matrix. Then we deduce collinear vector (a vector multiplied by a scalar value called characteristic value of a matrix or linear transformation).
The software MIDAS is the author’s development [14]. Mathematical software MIDAS is developed with the support of the Russian Foundation for basic research (project 14-01-00054).
At first, when calculating we used 18 indicators-factors, then we selected first seven factors to develop the model according to the number of its own factor, taking into account the effect of the factor on the unpaid loans. The results are in Table 4.
Calculated values of the variables in Table 3 show that the actual parameters “age” and “scope of activities” are the least significant. We should exclude “insignificant” factors for the regression model to describe accurately the risks of loan default, so we obtain the regression equation that contains all significant factors to measure values of credit nonpayment. The model includes the influence of the factors: “marital status” (x2), "number of dependents" (x3), “qualifications” (x5), “work experience” (x6), “monthly income” (x7).
This statistically significant regression equation has the form (formula 3):
Y= e(α0+ α1 x1+ α2 x2+ α3 x3+ α4 x4+ α5 x5+ α6 x6+ α7 x7)          (4)
where x2 – marital status;
x3 – number of dependents;
x5 – qualifications;
x6 – work experience;
x7 – monthly income;
y – repayment risk.

Quality Assessment of the Developed Regression Models
The quality of the model is assessed by standard way for regression models: using the coefficient of determination which is equal to 0,8347. The prediction accuracy of the regression model is measured by comparing the predicted and actual values of the repayment risk for test sampling adequacy and accuracy based on a regression analysis [15].
The formula 4 determines the forecast error:
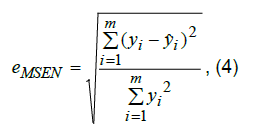where m – the number of observations, y i– the actual values, y ˆi– predicted values. For regression model, the forecasting error on the test sample is 36%, which is an acceptable value for such objectives.
The analysis shows to what degree the chosen method for estimating the coefficients is appropriate [12].
To compare the actual bank losses on real contracts with customers that vary in age, social and business activity, with their calculated values by the proposed model, we convert the numerical values (y) (Table 3) in the exponent. Table 5 shows calculation results.
Calculated by developed regression model values of losses almost coincide with the actual losses on real banking contracts.

KEY RESULTS
To forecast loan defaults from individuals to a commercial bank it’s proposed to use regression model based on the principal component analysis. The purpose of this model is to identify the relationship between the parameters (the independent variables), describing, on the one hand, business and social activity of the client, as factors of its financial reliability, on the other hand, the borrower's ability to be liable for debts [16].
The model reflects the relationship between significant independent factors characterizing the degree of the borrower’s financial reliability according to the component analysis method based on the model of David Cox. To analyze borrower’s status we used the following independent variables (parameters) as the borrower’s age, marriage status, and amount of dependents, sphere of activity, qualifications, work experience, and the average monthly revenue. To calculate principal components we use the program “MIDAS” which allows developing an accurate model, excluding the “insignificant” factors.
There is an insignificant difference between real credit losses and calculated values through the model of David Cox. Therefore, this model is suitable for forecasting loan defaults from individuals to a commercial bank in order to calculate how much the Bank will need high-quality borrowers to cover loss-making expired contracts in advance.

DISCUSSIONS
Predicting borrowers’ behavior and their ability to settle obligations is confide to the study of credit history scoring and results analysis, which based on banks’ scoring for internal use, as well as collecting information about customers’ income [17]. This method does not estimate variety of borrowers’ business and social characteristics and their influence on the financial reliability of customers and frequently there is no correlation between characteristics.
Factors that determine the effectiveness of making management decisions in making deals are dynamism, instability and uncertainty of the external environment [18]. It is connected with the sanctions imposed by Governments and foreign banks, geopolitical disagreements with partners at state level. Therefore, we should develop new approaches, methods and tools, analysis and forecast credit risks.
For solving such problems, it is necessary to apply such tools that helps to establish and to measure causal links among different features that characterize the internal and external socio-economic systems, including the banking system [19,20]. One of such tools is the principal component analysis method used for grouping basic data, when the elements within a group correlate to each other, but the whole group may be completely independent of other groups [11], for example, a group of social and economic factors.
This grouping allows to represent the subject’s behavior as a set of independent (statistically) components, which can be analyzed separately. Moreover, the factors within the group can influence each other. The relationship between factors can be both positive and negative (when the increase of the factor leads to decrease of another factor) [11].
Increasing of researched factors can improve the accuracy and quality of forecasting that influence on reasonability management decisions. In this regard, there is a possibility to forecast condition of socio-economic systems and processes, including the processes of lending to individuals, multifactorial mathematical models, allowing increasing if necessary the number of factorial signs [21]. Minimum limited factor features change at any time in each Bank. For example, if the Bank's credit portfolio contains expired agreements, the Bank raises the benchmark estimates of the factor indicators to get the best borrowers and to cover the current losses.

CONCLUSION
The developed model can serve as a base to predict repayment risk concluding agreements with individuals. It gives the opportunity to evaluate credit risks and manage them according to available information.
Practical use of the proposed model is an opportunity to study the behavior of borrowers using a mathematical model, presented in the form of a set of independent factors that characterize their social and business activity. These independent factors tracking in the automated program allow you to apply the method of principal components for subsequent regression models describing the influence of main factors on a productive indicator.
Recommendations of using principal component analysis method for developing regression customers’ behavior models, depending on their different characteristics, can be applied not only at the making loan agreement, but also in the course of its execution, because of customers’ information changeability. The monitoring is for softening condition of crediting and may be the competitive advantage of the Bank in lending to individuals.

Tables at a glance
Table icon Table icon Table icon Table icon Table icon
Table 1 Table 2 Table 3 Table 4 Table 5
 

Figures at a glance
Figure 1
Figure 1
 

References
Journal of Internet Banking and Commerce

Copyright © 2024 Research and Reviews, All Rights Reserved

www.jffactory.net